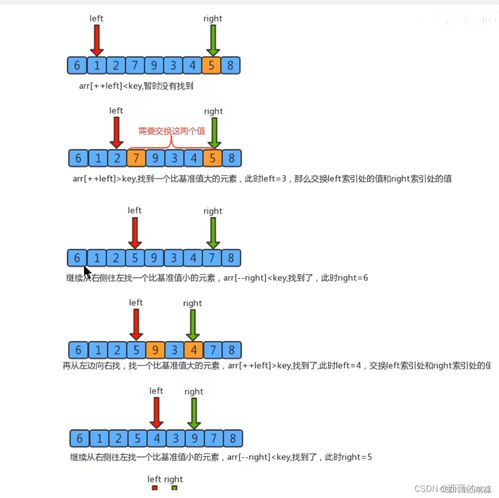
一、快速排序的基本原理
快速排序的核心思想是分治法。算法通过选取一个基准值(pivot),将数组分为两个子数组:小于基准值的元素和大于基准值的元素。这个过程递归进行,直到子数组的大小为1或0,此时数组已经排序完成。基本的快速排序算法在某些情况下可能会表现出较差的性能,因此需要进行优化。
二、优化策略之一:选择合适的基准值
选择合适的基准值是优化快速排序的关键。通常,基准值的选择有三种策略:固定基准值、随机基准值和三数中值分割法。三数中值分割法通常性能较好,它选择数组的头部、中间和尾部三个元素的中位数作为基准值,可以有效减少最坏情况出现的概率。
三、优化策略之二:处理小数组
对于小数组,快速排序的性能可能不如插入排序。因此,在快速排序算法中加入对小数组的特殊处理,当数组大小小于某个阈值(如10)时,使用插入排序来完成排序工作,可以提高整体性能。
四、优化策略之三:尾递归优化
尾递归优化是减少递归调用栈深度的有效方法。在快速排序中,通过调整递归顺序,优先递归处理较小的子数组,再迭代处理较大的子数组,可以减少递归调用的次数,从而降低内存消耗。
五、优化策略之四:迭代代替递归
虽然快速排序通常使用递归实现,但也可以通过迭代来避免递归带来的栈溢出风险。迭代版本的快速排序使用堆栈来模拟递归调用,这种方法在处理大数据集时更为稳定。
六、优化策略之五:消除重复元素
在含有大量重复元素的数组中,快速排序的性能可能会下降。通过在分区过程中消除重复元素,可以减少不必要的比较和交换,从而提高排序效率。
优化快速排序是提升算法性能的重要途径。通过选择合适的基准值、处理小数组、尾递归优化、迭代代替递归以及消除重复元素等策略,可以显著提高快速排序在各种数据情况下的性能。掌握这些优化技巧,将有助于我们在实际应用中更有效地利用快速排序算法。






评论列表